Our Problem in Pictures

I thought it might be interesting and instructive to visualize the ongoing debate over how to solve our debt and deficit problems, so I’ve taken to FRED to put some of these issues in pictures.

Before getting to that, though, I’d like to go on the record to state that I think any politician — Democrat or Republican — who signs a pledge (any pledge) is making a huge mistake, for the simple reason that there are only two ways to deal with having made such a commitment:  either one abides by it, or one reneges on it.  It forecloses on the notion of compromise, the key ingredient to getting things done in Washington.  Beyond that, it’s fairly juvenile, and I look forward to the day when our politicians will bind themselves via pinky swears and/or double-dares.  Really, it’s all so third grade.

Second, let’s talk about whether we have a “spending” problem or a “revenue” problem.  Since politicians — up to and including President Obama — like to equate the federal government to the average family (a truly pathetic comparison), let’s look at it in that light:  Say your household is spending $70,000/year on a $100,000/year gross (pre-tax) household income.  Well, it’s easy to say you have a “spending” problem that would be solved if you took your spending down to, say, $40,000/year.  Conversely, though, you might also solve the “problem” by getting a new job for $140,000/year (not saying that’s easy, of course, but certainly possible).  The notion — espoused by countless politicians — that the problem resides solely on spending and not also on revenues is absurd on its face.  Catherine Rampell has a very nice piece about this over at the NY Times website:  “But there is, in theory, a happy solution to our debt troubles. It’s called economic growth.  No need to raise taxes or cut programs.  Just get the economy growing the way it used to.” Indeed.

Okay, that said, let’s look at some charts that crystallize our predicament.

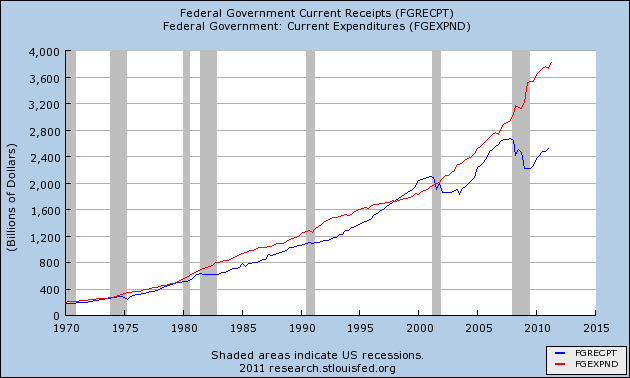
Above are current government receipts and expenditures.  The area leading into 2001 recession — where the blue line breaks above the red — is the period during which we were running surpluses, which was regrettably very short-lived.  The gap now is, clearly, the largest it’s been during the period I presented, but it strikes me as absurd to try closing it solely by focussing on the red line while simply ignoring the blue (the position being taken by certain pledge-takers).  As commenter Joel826 pointed out in the recent Rosie v Krugman discussion, professor Krugman has correctly pointed out that Fractions Have Denominators!  Obsessing over only the numerator or denominator in any ratio instead of looking at both is — I’m sorry to say it again — juvenile, but seems to be exactly what some pledge-signers are determined to do.

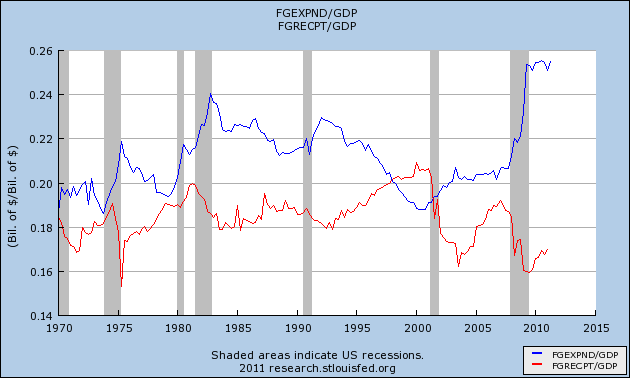
Let’s look at the data above in a bit of a different context — expenditures and receipts as a percent of GDP:

Going back to 1947 (not seen in the chart above), expenditures have run, on average, 19.6% of GDP while receipts have run, on average, 18.0% of GDP.  Which is to say that, historically, we’ve generally spent a bit more than we’ve taken in relative to GDP (visible below).  (Again, the surplus is clearly visible in the area circa 2000, where the red line breaks above the blue.)

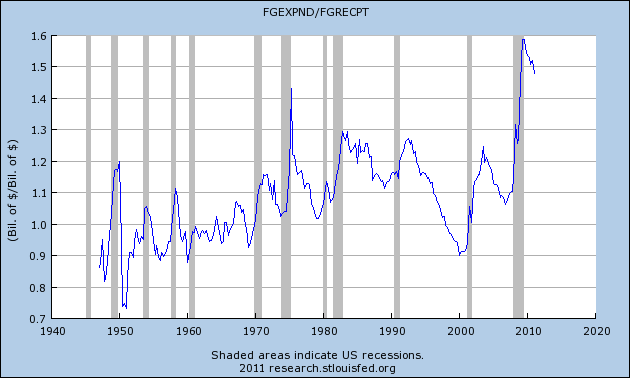
Relative to each other, here’s a historical look at how much we take in versus how much we spend:

It would appear we’ve peaked and begun trending lower here, although adding a trendline would produce a disturbing result, to be sure.  In any event, as expenditures decline (stimulus done, wind down the wars, etc.) and revenues rise, the chart above captures the essence of what Catherine Rampell was getting at in her story — we could grow our way out of our problems…if we could only grow!

Now here’s a look at the public debt and its relationship to GDP — Debt/GDP will surely soon cross 100%, as we have all been told repeatedly.  But again, I’m quick to point out that Debt/GDP is a ratio that is influenced by both its numerator and its denominator.  We can — and should — shrink the numerator while simultaneously growing the denominator.

I’ve got nothing profound to say about the situation, other than my belief that compromise always seems a better route than intransigence.