Top Economists Say War Is Bad for the Economy

Image courtesy of Steve Hess

War Makes Us Poor … And Drags the Economy Down Through the Floor

Preface: Many Americans – including influential economists and talking heads – still wrongly assume that war is good for the economy. For example, extremely influential economists like Paul Krugman and Martin Feldstein promote the myth that war is good for the economy.

Many congressmen assume that cutting pork-barrel military spending would hurt their constituents’ jobs. And talking heads like senior Washington Post political columnist David Broder parrot this idea.

As demonstrated below, it isn’t true.

Nobel-prize winning economist Joseph Stiglitz says that war is bad for the economy:

Stiglitz wrote in 2003:

War is widely thought to be linked to economic good times. The second world war is often said to have brought the world out of depression, and war has since enhanced its reputation as a spur to economic growth. Some even suggest that capitalism needs wars, that without them, recession would always lurk on the horizon. Today, we know that this is nonsense. The 1990s boom showed that peace is economically far better than war. The Gulf war of 1991 demonstrated that wars can actually be bad for an economy.

Stiglitz has also said that this decade’s Iraq war has been very bad for the economy. See this, this and this.

Former Federal Reserve chairman Alan Greenspan also said in that war is bad for the economy. In 1991, Greenspan said that a prolonged conflict in the Middle East would hurt the economy. And he made this point again in 1999:

Societies need to buy as much military insurance as they need, but to spend more than that is to squander money that could go toward improving the productivity of the economy as a whole: with more efficient transportation systems, a better educated citizenry, and so on. This is the point that retiring Rep. Barney Frank (D-Mass.) learned back in 1999 in a House Banking Committee hearing with then-Federal Reserve Chairman Alan Greenspan. Frank asked what factors were producing our then-strong economic performance. On Greenspan’s list: “The freeing up of resources previously employed to produce military products that was brought about by the end of the Cold War.” Are you saying, Frank asked, “that dollar for dollar, military products are there as insurance … and to the extent you could put those dollars into other areas, maybe education and job trainings, maybe into transportation … that is going to have a good economic effect?” Greenspan agreed.

Economist Dean Baker notes:

It is often believed that wars and military spending increases are good for the economy. In fact, most economic models show that military spending diverts resources from productive uses, such as consumption and investment, and ultimately slows economic growth and reduces employment.

Professor Emeritus of International Relations at the American University Joshua Goldstein notes:

Recurring war has drained wealth, disrupted markets, and depressed economic growth.

***

War generally impedes economic development and undermines prosperity.

And David R. Henderson – associate professor of economics at the Naval Postgraduate School in Monterey, California and previously a senior economist with President Reagan’s Council of Economic Advisers – writes:

Is military conflict really good for the economy of the country that engages in it? Basic economics answers a resounding “no.”

The Proof Is In the Pudding

Mike Lofgren notes:

Military spending may at one time have been a genuine job creator when weapons were compatible with converted civilian production lines, but the days of Rosie the Riveter are long gone. [Indeed, WWII was different from current wars in many ways, and so its economic effects are not comparable to those of today’s wars.] Most weapons projects now require relatively little touch labor. Instead, a disproportionate share is siphoned into high-cost R&D (from which the civilian economy benefits little), exorbitant management expenditures, high overhead, and out-and-out padding, including money that flows back into political campaigns. A dollar appropriated for highway construction, health care, or education will likely create more jobs than a dollar for Pentagon weapons procurement.

***

During the decade of the 2000s, DOD budgets, including funds spent on the war, doubled in our nation’s longest sustained post-World War II defense increase. Yet during the same decade, jobs were created at the slowest rate since the Hoover administration. If defense helped the economy, it is not evident. And just the wars in Iraq and Afghanistan added over $1.4 trillion to deficits, according to the Congressional Research Service. Whether the wars were “worth it” or merely stirred up a hornet’s nest abroad is a policy discussion for another time; what is clear is that whether you are a Keynesian or a deficit hawk, war and associated military spending are no economic panacea.

The Washington Post noted in 2008:

A recent paper from the National Bureau of Economic Research concludes that countries with high military expenditures during World War II showed strong economic growth following the war, but says this growth can be credited more to population growth than war spending. The paper finds that war spending had only minimal effects on per-capita economic activity.

***

A historical survey of the U.S. economy from the U.S. State Department reports the Vietnam War had a mixed economic impact. The first Gulf War typically meets criticism for having pushed the United States toward a 1991 recession.

The Institute for Economics & Peace (IEP) shows that any boost from war is temporary at best. For example, while WWII provided a temporary bump in GDP, GDP then fell back to the baseline trend. After the Korean War, GDP fell below the baseline trend:

IEP notes:

By examining the state of the economy at each of the major conflict periods since World War II, it can be seen that the positive effects of increased military spending were outweighed by longer term unintended negative macroeconomic consequences. While the stimulatory effect of military outlays is evidently associated with boosts in economic growth, adverse effects show up either immediately or soon after, through higher inflation, budget deficits, high taxes and reductions in consumption or investment. Rectifying these effects has required subsequent painful adjustments which are neither efficient nor desirable. When an economy has excess capacity and unemployment, it is possible that increasing military spending can provide an important stimulus. However, if there are budget constraints, as there are in the U.S. currently, then excessive military spending can displace more productive non-military outlays in other areas such as investments in high-tech industries, education, or infrastructure. The crowding-out effects of disproportionate government spending on military functions can affect service delivery or infrastructure development, ultimately affecting long-term growth rates.

***

Analysis of the macroeconomic components of GDP during World War II and in subsequent conflicts show heightened military spending had several adverse macroeconomic effects. These occurred as a direct consequence of the funding requirements of increased military spending. The U.S. has paid for its wars either through debt (World War II, Cold War, Afghanistan/Iraq), taxation (Korean War) or inflation (Vietnam). In each case, taxpayers have been burdened, and private sector consumption and investment have been constrained as a result. Other negative effects include larger budget deficits, higher taxes, and growth above trend leading to inflation pressure. These effects can run concurrent with major conflict or via lagging effects into the future. Regardless of the way a war is financed, the overall macroeconomic effect on the economy tends to be negative. For each of the periods after World War II, we need to ask, what would have happened in economic terms if these wars did not happen? On the specific evidence provided, it can be reasonably said, it is likely taxes would have been lower, inflation would have been lower, there would have been higher consumption and investment and certainly lower budget deficits. Some wars are necessary to fight and the negative effects of not fighting these wars can far outweigh the costs of fighting. However if there are other options, then it is prudent to exhaust them first as once wars do start, the outcome, duration and economic consequences are difficult to predict.

We noted in 2011:

This is a no-brainer, if you think about it. We’ve been in Afghanistan for almost twice as long as World War II. We’ve been in Iraq for years longer than WWII. We’ve been involved in 7 or 8 wars in the last decade. And yet [the economy is still unstable]. If wars really helped the economy, don’t you think things would have improved by now? Indeed, the Iraq war alone could end up costing more than World War II. And given the other wars we’ve been involved in this decade, I believe that the total price tag for the so-called “War on Terror” will definitely support that of the “Greatest War”.

Let’s look at the adverse effects of war in more detail …

War Spending Diverts Stimulus Away from the Real Civilian Economy

IEP notes that – even though the government spending soared – consumption and investment were flat during the Vietnam war:

The New Republic noted in 2009:

Conservative Harvard economist Robert Barro has argued that increased military spending during WWII actually depressed other parts of the economy.

(New Republic also points out that conservative economist Robert Higgs and liberal economists Larry Summers and Brad Delong have all shown that any stimulation to the economy from World War II has been greatly exaggerated.)

How could war actually hurt the economy, when so many say that it stimulates the economy?

Because of what economists call the “broken window fallacy”.

Specifically, if a window in a store is broken, it means that the window-maker gets paid to make a new window, and he, in turn, has money to pay others. However, economists long ago showed that – if the window hadn’t been broken – the shop-owner would have spent that money on other things, such as food, clothing, health care, consumer electronics or recreation, which would have helped the economy as much or more.

If the shop-owner hadn’t had to replace his window, he might have taken his family out to dinner, which would have circulated more money to the restaurant, and from there to other sectors of the economy. Similarly, the money spent on the war effort is money that cannot be spent on other sectors of the economy. Indeed, all of the military spending has just created military jobs, at the expense of the civilian economy.

Professor Henderson writes:

Money not spent on the military could be spent elsewhere.This also applies to human resources. The more than 200,000 U.S. military personnel in Iraq and Afghanistan could be doing something valuable at home.

Why is this hard to understand? The first reason is a point 19th-century French economic journalist Frederic Bastiat made in his essay, “What Is Seen and What Is Not Seen.” Everyone can see that soldiers are employed. But we cannot see the jobs and the other creative pursuits they could be engaged in were they not in the military.

The second reason is that when economic times are tough and unemployment is high, it’s easy to assume that other jobs could not exist. But they can. This gets to an argument Bastiat made in discussing demobilization of French soldiers after Napoleon’s downfall. He pointed out that when government cuts the size of the military, it frees up not only manpower but also money. The money that would have gone to pay soldiers can instead be used to hire them as civilian workers. That can happen in three ways, either individually or in combination: (1) a tax cut; (2) a reduction in the deficit; or (3) an increase in other government spending.

***

Most people still believe that World War II ended the Great Depression …. But look deeper.

***

The government-spending component of GNP went for guns, trucks, airplanes, tanks, gasoline, ships, uniforms, parachutes, and labor. What do these things have in common? Almost all of them were destroyed. Not just these goods but also the military’s billions of labor hours were used up without creating value to consumers. Much of the capital and labor used to make the hundreds of thousands of trucks and jeeps and the tens of thousands of tanks and airplanes would otherwise have been producing cars and trucks for the domestic economy. The assembly lines in Detroit, which had churned out 3.6 million cars in 1941, were retooled to produce the vehicles of war. From late 1942 to 1945, production of civilian cars was essentially shut down.

And that’s just one example. Women went without nylon stockings so that factories could produce parachutes. Civilians faced tight rationing of gasoline so that U.S. bombers could fly over Germany. People went without meat so that U.S. soldiers could be fed. And so on.

These resources helped win the war—no small issue. But the war was not a stimulus program, either in its intentions or in its effects, and it was not necessary for pulling the U.S. out of the Great Depression. Had World War II never taken place, millions of cars would have been produced; people would have been able to travel much more widely; and there would have been no rationing. In short, by the standard measures, Americans would have been much more prosperous.

Today, the vast majority of us are richer than even the most affluent people back then. But despite this prosperity, one thing has not changed: war is bad for our economy. The $150 billion that the government spends annually on wars in Iraq and Afghanistan (and, increasingly, Pakistan) could instead be used to cut taxes or cut the deficit. By ending its ongoing wars … the U.S. government … would be developing a more prosperous economy.

Austrian economist Ludwig Von Mises points:

That is the essence of so-called war prosperity; it enriches some by what it takes from others. It is not rising wealth but a shifting of wealth and income.

We noted in 2010:

You know about America’s unemployment problem. You may have even heard that the U.S. may very well have suffered a permanent destruction of jobs.

But did you know that the defense employment sector is booming?

[P]ublic sector spending – and mainly defense spending – has accounted for virtually all of the new job creation in the past 10 years:

The U.S. has largely been financing job creation for ten years. Specifically, as the chief economist for BusinessWeek, Michael Mandel, points out, public spending has accounted for virtually all new job creation in the past 1o years:

Private sector job growth was almost non-existent over the past ten years. Take a look at this horrifying chart:

Between May 1999 and May 2009, employment in the private sector sector only rose by 1.1%, by far the lowest 10-year increase in the post-depression period.

It’s impossible to overstate how bad this is. Basically speaking, the private sector job machine has almost completely stalled over the past ten years. Take a look at this chart:

Over the past 10 years, the private sector has generated roughly 1.1 million additional jobs, or about 100K per year. The public sector created about 2.4 million jobs.

But even that gives the private sector too much credit. Remember that the private sector includes health care, social assistance, and education, all areas which receive a lot of government support.

***

Most of the industries which had positive job growth over the past ten years were in the HealthEdGov sector. In fact, financial job growth was nearly nonexistent once we take out the health insurers.

Let me finish with a final chart.

Without a decade of growing government support from rising health and education spending and soaring budget deficits, the labor market would have been flat on its back. [120]

***

So most of the job creation has been by the public sector. But because the job creation has been financed with loans from China and private banks, trillions in unnecessary interest charges have been incurred by the U.S.

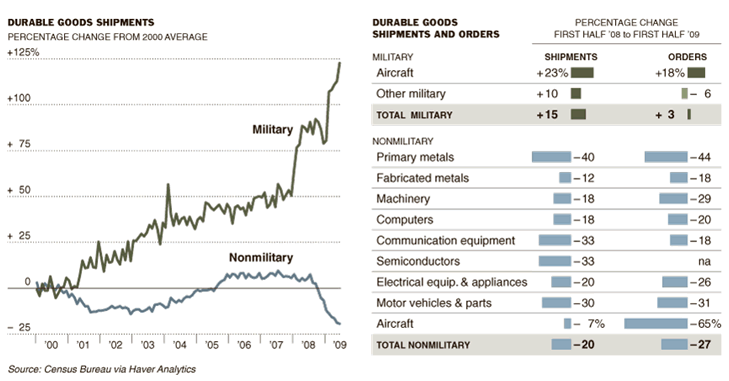
And this shows military versus non-military durable goods shipments: [Click here to view full image.]

So we’re running up our debt (which will eventually decrease economic growth), but the only jobs we’re creating are military and other public sector jobs.

PhD economist Dean Baker points out that America’s massive military spending on unnecessary and unpopular wars lowers economic growth and increases unemployment:

Defense spending means that the government is pulling away resources from the uses determined by the market and instead using them to buy weapons and supplies and to pay for soldiers and other military personnel. In standard economic models, defense spending is a direct drain on the economy, reducing efficiency, slowing growth and costing jobs.

A few years ago, the Center for Economic and Policy Research commissioned Global Insight, one of the leading economic modeling firms, to project the impact of a sustained increase in defense spending equal to 1.0 percentage point of GDP. This was roughly equal to the cost of the Iraq War.

Global Insight’s model projected that after 20 years the economy would be about 0.6 percentage points smaller as a result of the additional defense spending. Slower growth would imply a loss of almost 700,000 jobs compared to a situation in which defense spending had not been increased. Construction and manufacturing were especially big job losers in the projections, losing 210,000 and 90,000 jobs, respectively.

The scenario we asked Global Insight [recognized as the most consistently accurate forecasting company in the world] to model turned out to have vastly underestimated the increase in defense spending associated with current policy. In the most recent quarter, defense spending was equal to 5.6 percent of GDP. By comparison, before the September 11th attacks, the Congressional Budget Office projected that defense spending in 2009 would be equal to just 2.4 percent of GDP. Our post-September 11th build-up was equal to 3.2 percentage points of GDP compared to the pre-attack baseline. This means that the Global Insight projections of job loss are far too low…

The projected job loss from this increase in defense spending would be close to 2 million. In other words, the standard economic models that project job loss from efforts to stem global warming also project that the increase in defense spending since 2000 will cost the economy close to 2 million jobs in the long run.

The Political Economy Research Institute at the University of Massachusetts, Amherst has also shown that non-military spending creates more jobs than military spending.

So we’re running up our debt – which will eventually decrease economic growth – and creating many fewer jobs than if we spent the money on non-military purposes.

High Military Spending Drains Innovation, Investment and Manufacturing Strength from the Civilian Economy

Chalmers Johnson notes that high military spending diverts innovation and manufacturing capacity from the economy:

By the 1960s it was becoming apparent that turning over the nation’s largest manufacturing enterprises to the Department of Defense and producing goods without any investment or consumption value was starting to crowd out civilian economic activities. The historian Thomas E Woods Jr observes that, during the 1950s and 1960s, between one-third and two-thirds of all US research talent was siphoned off into the military sector. It is, of course, impossible to know what innovations never appeared as a result of this diversion of resources and brainpower into the service of the military, but it was during the 1960s that we first began to notice Japan was outpacing us in the design and quality of a range of consumer goods, including household electronics and automobiles.

***

Woods writes: “According to the US Department of Defense, during the four decades from 1947 through 1987 it used (in 1982 dollars) $7.62 trillion in capital resources. In 1985, the Department of Commerce estimated the value of the nation’s plant and equipment, and infrastructure, at just over $7.29 trillion… The amount spent over that period could have doubled the American capital stock or modernized and replaced its existing stock”.

The fact that we did not modernise or replace our capital assets is one of the main reasons why, by the turn of the 21st century, our manufacturing base had all but evaporated. Machine tools, an industry on which Melman was an authority, are a particularly important symptom. In November 1968, a five-year inventory disclosed “that 64% of the metalworking machine tools used in US industry were 10 years old or older. The age of this industrial equipment (drills, lathes, etc.) marks the United States’ machine tool stock as the oldest among all major industrial nations, and it marks the continuation of a deterioration process that began with the end of the second world war. This deterioration at the base of the industrial system certifies to the continuous debilitating and depleting effect that the military use of capital and research and development talent has had on American industry.”

Economist Robert Higgs makes the same pointabout World War II:

Yes, officially measured GDP soared during the war. Examination of that increased output shows, however, that it consisted entirely of military goods and services. Real civilian consumption and private investment both fell after 1941, and they did not recover fully until 1946. The privately owned capital stock actually shrank during the war. Some prosperity. (My article in the peer-reviewed Journal of Economic History, March 1992, presents many of the relevant details.)

It is high time that we come to appreciate the distinction between the government spending, especially the war spending, that bulks up official GDP figures and the kinds of production that create genuine economic prosperity. As Ludwig von Mises wrote in the aftermath of World War I, “war prosperity is like the prosperity that an earthquake or a plague brings.”

War Causes Inflation … Which Keynes and Bernanke Admit Taxes Consumers

As we noted in 2010, war causes inflation … which hurts consumers:

Liberal economist James Galbraith wrote in 2004:

Inflation applies the law of the jungle to war finance. Prices and profits rise, wages and their purchasing power fall. Thugs, profiteers and the well connected get rich. Working people and the poor make out as they can. Savings erode, through the unseen mechanism of the “inflation tax” — meaning that the government runs a big deficit in nominal terms, but a smaller one when inflation is factored in.

***

There is profiteering. Firms with monopoly power usually keep some in reserve. In wartime, if the climate is permissive, they bring it out and use it. Gas prices can go up when refining capacity becomes short — due partly to too many mergers. More generally, when sales to consumers are slow, businesses ought to cut prices — but many of them don’t. Instead, they raise prices to meet their income targets and hope that the market won’t collapse.

Ron Paul agreed in 2007:

Congress and the Federal Reserve Bank have a cozy, unspoken arrangement that makes war easier to finance. Congress has an insatiable appetite for new spending, but raising taxes is politically unpopular. The Federal Reserve, however, is happy to accommodate deficit spending by creating new money through the Treasury Department. In exchange, Congress leaves the Fed alone to operate free of pesky oversight and free of political scrutiny. Monetary policy is utterly ignored in Washington, even though the Federal Reserve system is a creation of Congress.

The result of this arrangement is inflation. And inflation finances war.

Blanchard Economic Research pointed out in 2001:

War has a profound effect on the economy, our government and its fiscal and monetary policies. These effects have consistently led to high inflation.

***

David Hackett Fischer is a Professor of History and Economic History at Brandeis. [H]is book, The Great Wave, Price Revolutions and the Rhythm of History … finds that … periods of high inflation are caused by, and cause, a breakdown in order and a loss of faith in political institutions. He also finds that war is a triggering influence on inflation, political disorder, social conflict and economic disruption.

***

Other economists agree with Professor Fischer’s link between inflation and war.

James Grant, the respected editor of Grant’s Interest Rate Observer, supplies us with the most timely perspective on the effect of war on inflation in the September 14 issue of his newsletter:

“War is inflationary. It is always wasteful no matter how just the cause. It is cost without income, destruction financed (more often than not) by credit creation. It is the essence of inflation.”

Libertarian economics writer Lew Rockwell noted in 2008:

You can line up 100 professional war historians and political scientists to talk about the 20th century, and not one is likely to mention the role of the Fed in funding US militarism. And yet it is true: the Fed is the institution that has created the money to fund the wars. In this role, it has solved a major problem that the state has confronted for all of human history. A state without money or a state that must tax its citizens to raise money for its wars is necessarily limited in its imperial ambitions. Keep in mind that this is only a problem for the state. It is not a problem for the people. The inability of the state to fund its unlimited ambitions is worth more for the people than every kind of legal check and balance. It is more valuable than all the constitutions every devised.

***

Reflecting on the calamity of this war, Ludwig von Mises wrote in 1919

One can say without exaggeration that inflation is an indispensable means of militarism. Without it, the repercussions of war on welfare become obvious much more quickly and penetratingly; war weariness would set in much earlier.***

 

In the entire run-up to war, George Bush just assumed as a matter of policy that it was his decision alone whether to invade Iraq. The objections by Ron Paul and some other members of Congress and vast numbers of the American population were reduced to little more than white noise in the background. Imagine if he had to raise the money for the war through taxes. It never would have happened. But he didn’t have to. He knew the money would be there. So despite a $200 billion deficit, a $9 trillion debt, $5 trillion in outstanding debt instruments held by the public, a federal budget of $3 trillion, and falling tax receipts in 2001, Bush contemplated a war that has cost $525 billion dollars — or $4,681 per household. Imagine if he had gone to the American people to request that. What would have happened? I think we know the answer to that question. And those are government figures; the actual cost of this war will be far higher — perhaps $20,000 per household.

***

If the state has the power and is asked to choose between doing good and waging war, what will it choose? Certainly in the American context, the choice has always been for war.

And progressive economics writer Chris Martenson explains as part of his “Crash Course” on economics:

If we look at the entire sweep of history, we can make an utterly obvious claim: All wars are inflationary. Period. No exceptions.

***

So if anybody tries to tell you that you haven’t sacrificed for the war, let them know you sacrificed a large portion of your savings and your paycheck to the effort, thank you very much.

The bottom line is that war always causes inflation, at least when it is funded through money-printing instead of a pay-as-you-go system of taxes and/or bonds. It might be great for a handful of defense contractors, but war is bad for Main Street, stealing wealth from people by making their dollars worth less.

Given that John Maynard Keynes and former Federal Reserve chair Ben Bernanke both say that inflation is a tax on the American people, war-induced inflation is a theft of our wealth.

IEP gives a graphic example – the Vietnam war helping to push inflation through the roof:

War Causes Runaway Debt

We noted in 2010:

All of the spending on unnecessary wars adds up.

The U.S. is adding trillions to its debt burden to finance its multiple wars in Iraq, Afghanistan, Yemen, etc.

Indeed, IEP – commenting on the war in Afghanistan and Iraq – notes:

This was also the first time in U.S. history where taxes were cut during a war which then resulted in both wars completely financed by deficit spending. A loose monetary policy was also implemented while interest rates were kept low and banking regulations were relaxed to stimulate the economy. All of these factors have contributed to the U.S. having severe unsustainable structural imbalances in its government finances.

We also pointed out in 2010:

It is ironic that America’s huge military spending is what made us an empire … but our huge military is what is bankrupting us … thus destroying our status as an empire.

Economist Michel Chossudovsky told Washington’s Blog:

War always causes recession. Well, if it is a very short war, then it may stimulate the economy in the short-run. But if there is not a quick victory and it drags on, then wars always put the nation waging war into a recession and hurt its economy.

Indeed, we’ve known for 2,500 years that prolonged war bankrupts an economy (and remember Greenspan’s comment.)

It’s not just civilians saying this …

The former head of the Joint Chiefs of Staff – Admiral Mullen – agrees:

The Pentagon needs to cut back on spending.

“We’re going to have to do that if it’s going to survive at all,” Mullen said, “and do it in a way that is predictable.”

Indeed, Mullen said:

For industry and adequate defense funding to survive … the two must work together. Otherwise, he added, “this wave of debt” will carry over from year to year, and eventually, the defense budget will be cut just to facilitate the debt.

Former Secretary of Defense Robert Gates agrees as well. As David Ignatius wrote in the Washington Post in 2010:

After a decade of war and financial crisis, America has run up debts that pose a national security problem, not just an economic one.

***

One of the strongest voices arguing for fiscal responsibility as a national security issue has been Defense Secretary Bob Gates. He gave a landmark speech in Kansas on May 8, invoking President Dwight Eisenhower’s warnings about the dangers of an imbalanced military-industrial state.

“Eisenhower was wary of seeing his beloved republic turn into a muscle-bound, garrison state — militarily strong, but economically stagnant and strategically insolvent,” Gates said. He warned that America was in a “parlous fiscal condition” and that the “gusher” of military spending that followed Sept. 11, 2001, must be capped. “We can’t have a strong military if we have a weak economy,” Gates told reporters who covered the Kansas speech.

On Thursday the defense secretary reiterated his pitch that Congress must stop shoveling money at the military, telling Pentagon reporters: “The defense budget process should no longer be characterized by ‘business as usual’ within this building — or outside of it.”

While war might make a handful in the military-industrial complex and big banks rich, America’s top military leaders and economists say that would be a very bad idea for the American people.

Indeed, military strategists have known for 2,500 years that prolonged wars are disastrous for the nation.

War Increases Terrorism … And Terrorism Hurts the Economy

Security experts – conservative hawks and liberal doves alike – agree that waging war in the Middle East weakens national security and increases terrorism. See this, this, this, this, this, this and this.

Terrorism – in turn – terrorism is bad for the economy. Specifically, a study by Harvard and the National Bureau of Economic Research (NBER) points out:

From an economic standpoint, terrorism has been described to have four main effects (see, e.g., US Congress, Joint Economic Committee, 2002). First, the capital stock (human and physical) of a country is reduced as a result of terrorist attacks. Second, the terrorist threat induces higher levels of uncertainty. Third, terrorism promotes increases in counter-terrorism expenditures, drawing resources from productive sectors for use in security. Fourth, terrorism is known to affect negatively specific industries such as tourism.

The Harvard/NBER concludes:

In accordance with the predictions of the model, higher levels of terrorist risks are associated with lower levels of net foreign direct investment positions, even after controlling for other types of country risks. On average, a standard deviation increase in the terrorist risk is associated with a fall in the net foreign direct investment position of about 5 percent of GDP.

So the more unnecessary wars American launches and the more innocent civilians we kill, the less foreign investment in America, the more destruction to our capital stock, the higher the level of uncertainty, the more counter-terrorism expenditures and the less expenditures in more productive sectors, and the greater the hit to tourism and some other industries. Moreover:

Terrorism has contributed to a decline in the global economy (for example, European Commission, 2001).

So military adventurism increases terrorism which hurts the world economy. And see this.

Postscript: Attacking a country which controls the flow of oil has special impacts on the economy. For example, well-known economist Nouriel Roubini says that attacking Iran would lead to global recession. The IMF says that Iran cutting off oil supplies could raise crude prices 30%.