One of the most fascinating things about markets is the sheer volume of data they generate. Every day, millions of data points get created. The vast majority of this amounts to little more than noise. This endless stream of information leads thousands of us everyday on a hunt for meaningful signal amid the cacophony.
Most of the time, we are unsuccessful. We can be tricked into seeing significance where none exists. Our pattern recognition engines are fooled by what turns out to be mere randomness (there’s a good idea for a book in that). There is a meaningful needle buried somewhere in the haystack of numbers, but we underestimate both how hard it is to identify, and just how huge that stack is.
As an example, let’s take a number we are all familiar with: Average market returns. Depending upon the period of the data set under discussion, we usually envision a long-term annualized compound return of 8 percent to 10 percent.
Have a look at the chart below:
Distribution of S&P 500 Returns During Calendar Years 1926–2014
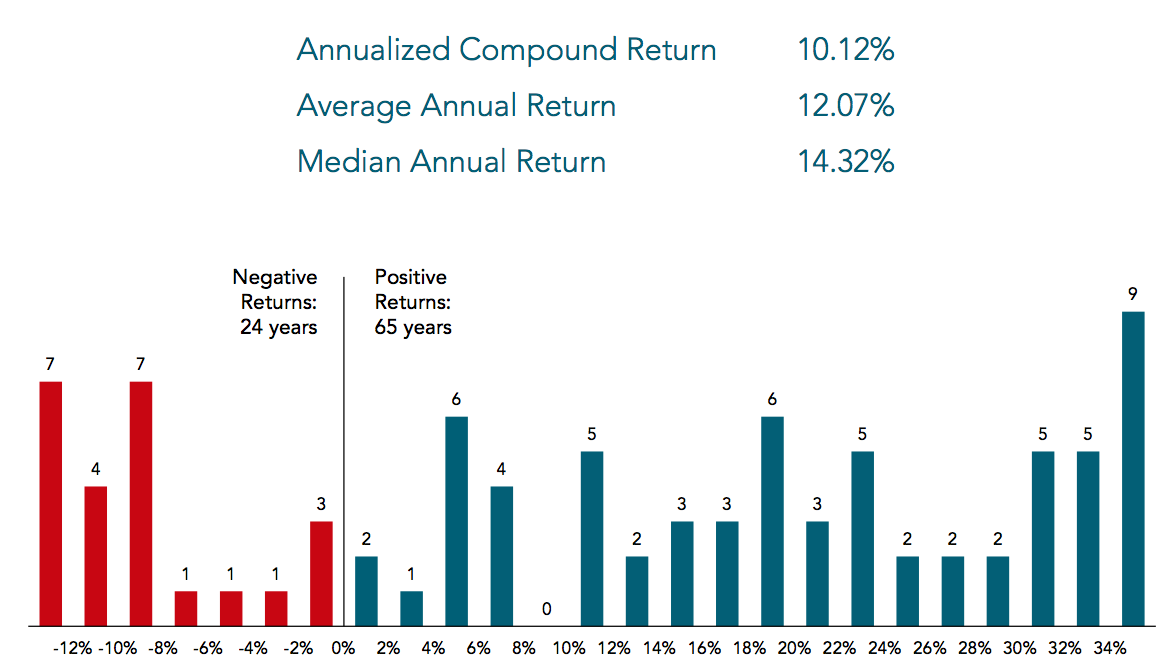
Source: Dimensional Funds
Continues here: Average Returns, Rarer Than You Think


Isn’t this another way of looking at Buffett’s rules of investing?
Rule #1 Don’t lose money.
Rule #2 Don’t forget rule #1.
If we eliminate the negative returns in the above chart, the mid-point of what remains comes in pretty close to Buffett’s long-term track record …
me thinks looking at rolling 12 month returns vs calendar year returns would be more useful — perhaps not dramatically alter conclusion but seems to make more sense
O.K., I’m confused. Does the -12% column represent all years that were -12% or worse?
That looks like a normal distribution to me that would be very amenable to statistical analysis based on the mean return.
Call me Sherlock (well, it is the Internet, so you’ll probably call me something wondrously rude instead), but it seems the most likely return, 8-10%, has not happened. Isn’t randomness fantastic. And probability is so much fun as well (I read a whole book on the Monty Hall question – what a waste of time, but happily wasted time, that was).