Salil Mehta is a two-time Administration executive, leading Treasury/TARP’s analytics team, as well as PBGC’s policy, research, and analysis, as well as their first risk analysis function. Salil is the creator of one of the most popular free statistics blogs, Statistical Ideas.
~~~
For just a couple bucks, you might win money to last your lifetime. Plus we have seductive mottos such as “Someone’s going to lotto”, so why not? Recent jackpots have also staggered near very high levels (the record $1.6 billion dollars in January 2016, and also twice ~$300 million dollars since then including now), and this has caused many otherwise rational people to tune in to the mania and try their hand at this gambit. We also see in the recent data that many more people are turning towards the Lottery for their financial solutions, since the global financial crisis. The mere fact that people worldwide would be more drawn to “play”, when the jackpot is in the hundreds of millions or more, versus when it is “only” in the low millions, provides a frenzy of opportunity to study the exciting probability concepts within the Lottery. The conclusions inevitably are still not vague, especially when you are not emotionally and financially invested in what amounts to an absurd, money-gouging scheme. One of the best counsels we have from this article is that you would be best to scrape up enough money each week to play the Lottery, but then insteadboomerang those funds back into your savings account and simply keep on working through retirement age. There is simply no expedited-track to success, particularly with the Lottery.
One should remember that the only objective for the Lottery, anywhere in the world, is not to make you rich. Contrary to their advertisements, the objective is not to show you a good time. Wasting your money is never a good time. The lottery’s only objective is to maximize the funds you pay for educational activities. The lottery does this by taking all of the proceeds, then first diverting nearly 45% of it towards educational benefits, and also towards store commissions and advertisements designed to trick you into spending more into the system. Say you played 292 million times with hypothetically a $1 ticket, and then won exactly one time. In this case your reward would not be anywhere close to $292m. The funnel would start at a gross level of just 55% of $292m (or a loss of $131m on your ticket purchases since 45% was skimmed straight away to the government). And then your net amount would still be less than this 55% gross payout, since this reward is again taxed as income. There is nothing sexy about this arrangement; it extorts a non-tax deductible dollar from you and many others, who could least afford it. And each time putting offering 55 cents into a community savings jar, until one day that amassed jar is given to basically just one person at random (but not before the government comes back to tax that jar as “income”). The whole scheme is an educational tax for those who instead could use a free education in probability theory (that’s where this blog comes in!)
We approach this article by focusing on several pertinent facets of the Lottery, holding of interest something for everyone:
- who is playing and the dispersion in government profits
- the probability of winning
- rebuttal to the Lottery’s official position
- the trends and strategies in lottery wins
- discussing number-picking strategies
- a final irony
Please read any or all of these six self-contained sections, as they are segmented below.
Who is playing and the dispersion in government profits
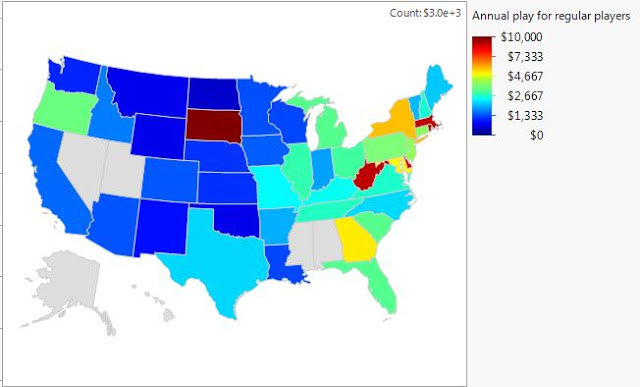
The dispersion in annual lottery revenue per state should be adjusted for the number of adults who are playing in that state. This then gives a reflection of the per person lottery play that is recently occurring. Getting to the number of regular-playing adults involves some probability estimation, since we are working with a large amount of anonymized data. And the calculation otherwise is similar to how a company would calculate FTEs from a pool of full-time and part-time employees. We start here by having a fairly accurately get to the number of adults eligible to play the Lottery in each state. And the Lottery provides crude estimates for the total eligible population who play the Lottery each year (~100 semi-weekly drawings). We can also see through the Pareto principle that suggests that not everyone who plays the Lottery, plays to the same extent (some buy more tickets than others). So we back into a conservative estimate for the ongoing number of tickets purchased by the average regularly playing adult per state. That’s what we are getting at in the chart below. Of the equivalent number of adults who regularly play in the United States (U.S.), the average level of ticket spending per year is roughly $3k! That’s a lot of money, and it’s not even homogenously spread across the U.S. States such as Massachusetts’s adult players command over 3 times this national level of ticket spending.
Now why would that be for Massachusetts, a great state housing two of the world’s foremost universities? Or is the causality going the other way: because of all of the Lottery playing in Massachusetts, universities such as Harvard have become so great? Obviously that doesn’t make sense.
Or maybe something else is going on, for example there is so much Massachusetts’ play because a lone MIT scientist is hastily rigging the system with, well, his or her smarts? And that wouldn’t be the first time during this millennium (here, here). But anyway, this is not right answer either.
A theory about market efficiency makes sense to bring up here. Let’s revisit our earlier discussion concerning how much revenue the government makes directly from these tickets. Examining the records from the available 44 states (plus the District of Columbia), we see that:
- 24 states have prize payouts between >60 cents, per dollar played. These 24 are in more populated states.
- 21 states have prize payouts between <60 cents, per dollar played. These 21 are in less populated states.
Perhaps the more populated states have multiple related factors working in their favor. They have efficiencies in scale and a diverse tax revenue stream, which allows it to offer more affordable lotteries against their state budgets. And generally at the same time, the playing adults in those states can and do “afford” larger lottery spending in these sometimes wealthier states. In truth they shouldn’t still afford it at all, but these are simply the patterns that strongly match-up. Last, larger states generally have larger jackpots in the regional lotteries, which attract more playing for that reason alone and may cause some higher payout affordability. We will discuss later in this article the interesting concept that as the purse money swells in any state for a short period, then the conditional payout swells to arbitrage it away.
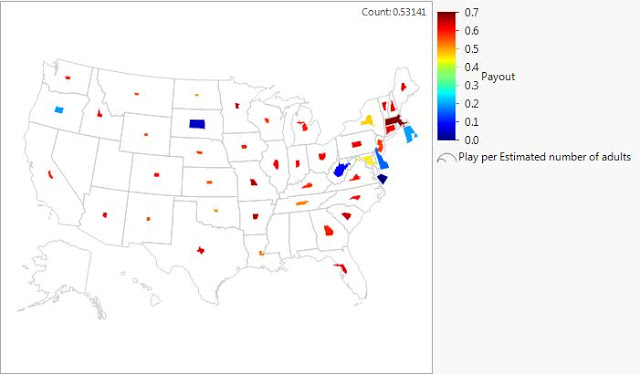
Besides looking at payout by frequency as we just discussed, we can look at the payout weighted (by total ticket sales) and we see it is more firmly below 60 cents, per dollar played. It is at nearly 53 cents per dollar, as shown below. Though in this chart we show the payout yet another way, by the tickets played per person and we see smaller playing relative to the larger population in these high-payout states.
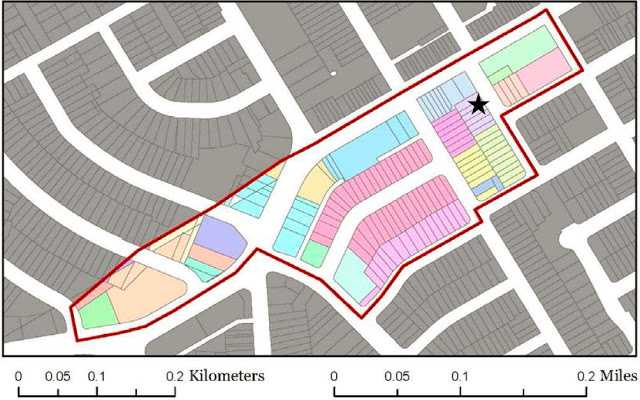
It is also important to note that looking at unemployment levels in the states or in the counties, has no relationship to the Lottery revenue. Hence economics tends not to be the dominant driver here. And in fact regional Federal Reserve research on a small sample of Canadian lottery winners shows that “dissemination areas” (i.e., homes) in close proximity to lottery winners tend to overspend their means in order to “catch up” with the instantaneously enhanced lifestyles of the winner. And hence at higher risk of bankruptcy that they otherwise might have avoided. See a version of the plots used below (the asterisk in this actual map was a lottery winner).
The probability of winning
Imagine the fun of catching a ball at a professional baseball game. These rare winners take home a trophy that would seem improbable for you specifically to do. Even though it seems as is a ball is being hit into the stands at every game. Now, imagine that only one ball is ever hit over the fence in any one of the U.S. ballparks, every few years. The likelihood of catching this one ball is suddenly even lower than it was before. Yet that probability now equals the current odds of winning the Lottery! Let’s dig into the actual probability formulae to see how we get to these odds.
A common framework for the original lottery is 69 white balls, of which you must select the 5 correct, unique balls. The probability of this occurring is a combinatorics (much discussed here, here, here) problem where we have 69 ways to select the 1st ball, followed by 68 ways to select the 2nd ball, etc. Also the sequence of the balls doesn’t matter for anyone, so that could be “factored out” as: there are 5 ways to order the 1stwinning ball, followed by there are 4 ways to order the 2nd ball, etc. Here are the odds in this hypothetical, 5-white ball only framework:
1 in 5C69
= 1 in 69!/(69-5)!/5!
= 1 in 69*68*67*66*65/5/4/3/2/1
= 1 in 11.2 million
Let’s pause here. Imagine that in this 5-white ball only lottery that we could target a single 100% payout jackpot of $11.2 million, sourced by on ongoing pool of 11.2 million adult players at $1 a ticket.
Now let’s say, for whatever reason, $11.2 million just doesn’t get people excited to come out and play, and so the Lottery is tasked to engineer an even higher prize. Something too big to fail! Welcome a separate urn of 26 hot-red “powerballs”. If one is to win the whole jackpot now, then the probability of this happening is 1 in 11.2m*26 (since one has to now has to jointly match the one correct powerball). Things are getting wild with this new powerball format, and this is precisely where the Lottery gets its stated odds of 1 in 292 million (11.2m*26 red-balls).
Also since the payout happens 26 times less frequently, the government can financially afford to enhance the jackpot by a little less than 26 times the original $11.2 million we solved for above (i.e., in the 5-white ball only example). At 26 times $11.2 million we get nearly $292 million! This is the essential probability and leverage that takes a jackpot -originally in the tens of millions- and pumps it up to hundreds of millions albeit with less frequent winnings. We’ll then also work on the “less frequent winnings” part next.
The math is going to get a little more complicated, even in this case of having winners select all 5 white balls (e.g., similar to the 5 white-ball only example above). The reason is that while we consolidated all the winnings to engineer a behemoth $292 million Powerball jackpot, it came at the expense of one winner every few months, instead of roughly one winner per drawing. Such momentum loss could be a downer, so the Lottery put in smaller “grab bags”, such as $1 million sub-prizes to anyone selecting “only” the 5-white balls but failed in selecting the red-powerball. We would expect that for every Powerball jackpot winner, there would be 25 main prize losers who would instead win the smaller prize for selecting the 5-white balls and missing the red-powerball. To afford these greater number of prizes, we must reduce the $292 million Powerball jackpot by only 25 times the $1 million intervening prize amounts (or a reduction to only $267 million from the Powerball grand prize).
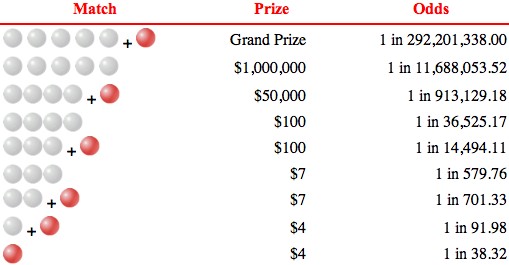
The probability of winning these smaller $1 million prizes would be 25 of 292 million of course, or 1 in 11.7 million. So this now explains the first 2 prize lines of this odds table pictured on the Lottery website: since we just showed above how we get to the 1:292m and the 1:11.7m probability results.
There is still the original 1:11.2 million chance to win the 5-white balls lottery, it’s just that this lottery was replaced with the introduction of the powerball. So the odds of winning a 5-white ball prize is no longer homogenous and there are 2 more competitive powerball prizes instead each with “slightly worse” odds (though winning either collectively returns one to the 1:11.2 million). The “worse” odds again are 1:292m for the bigger prize for also matching the powerball, and 1:11.7m for the smaller prize without the powerball match.
It is worth noting the 292 million players also happens to be roughly the size of the U.S. adult population (which is more like a quarter billion). Perhaps the sizings of the Lottery reflects something about the sizing of the underlying population, ensuring a decent optimal play level and robust winning occurrences (optimal for the Lottery though, not for you!)
Of course the easiest prize to win, with the full spectrum of Powerball sub-prizes shown above, is a match of only the powerball itself. Matching the powerball, without regard to any of the white balls, is of course a 1:26 chance. Which can also be thought of as 11.2 million “red-ball” winners, per 292 million plays.
We can change this probability framework around and appreciate that the chance of matching all 5-white balls, again, would be 26 such matches per 292 million plays. And it’s the intersection of one of those 26 5-white ball matches, and the one of those 11.2 million red-powerball matches, that creates only one exciting 1 in 292 million chance of winning the grand prize: simultaneously matching all 5-white balls and the one powerball!
Now say we have discussed so far a world, where there is only three prizes offered:
- one for matching the powerball-only
- one for matching all 5-white balls only (25 in 292 million)
- one grand prize for matching all 5-white balls plus the one powerball (1 in 292 million)
Then the odds of winning the red-powerball only (first bullet above) is:
(11.2 million – 1) / 292 million
= 1 in >26
In other words, there needs to be slightly more plays per winning red-powerball only prize, since one of those powerball matches instead counts only towards the outcome odds of winning the more exclusive larger jackpot (the one where the 5-white balls must also match). This is why the bottom prize line of the odds table pictured above shows that the powerball-only is 1:>26 odds. Not 1:26.
More importantly, the introduction of the powerball suddenly to the original lottery allows one to cheaply drive up the frequency of having any type of winnings, from originally 1 in 11.2 million if we kept the Lottery at only someone winning all 5-white balls. The Lottery can then slickly market to you that there is nearly a 1 in <30 chance of winning “a prize”. Even if that prize can’t even buy you a movie ticket.
For example, how fun, in our current real-life lottery, with all the sub-prizes added in, you have a one in 38 chance to win exactly, get ready now… $4 (and that’s before taxes)! Yes, you’ll spend nearly $72 (after taxes) though, to play those 38 times (and there is a >99% chance you won’t get anything other than one or two of those $4 prizes after spending $72 on those 38 attempts!) This is how the government more so that Wall Street, encourages you to be stupid, poor, and despondent.
With the size of the adult playing population the government sizes the Lottery through the means described above, so that they can scintillatingly create main prizes that can be optimally won, a few times a year, to just one winner (when approximately the prize happens to swell to the size of the adult U.S. population and with lottery gaming appetite this comes to a Powerball or Mega Million prize of about $300 million, which it was close when won by a sole winner in March 2016). Jointly, one also wants to ensure that there is also a healthy supply of cheap-to-fulfill “goody bags” for all the lower prizes to keep excitement on hand for the next go-around. The price to fund the red-ball only prize is just <$11.2 million, relative to a grand prize of <$292 million that is empirically ~8 times the starting grand prize. Since the $292 million was merely a theoretical hypothetical based upon a full play size. Also recall that $25 million in this case (25 of the $1 million 2ndprizes) was allotted to winners of the 5-white balls only matches; this is also funded from the same $292 million topline jackpot money.
With the introduction of these many smaller, intervening prizes (either through matching less white balls or the introduction of the red powerball concept) we see that the overall probability of winning any prize to increases slightly (we see in the Lottery odds table above that it is 1:25, instead of 1:26 or even 1:<26). Maximizing lottery revenue implies establishing all of the parameters above optimally, for a given lottery region. Note that even for the national lottery, there are small customizations such as with California players who enjoy smaller prizes that are set of variable levels instead of fixed. This allows those minority of states more finessed revenue tuning, yet more difficult probability calculations for the consumer to understand!
While discussing probability, we should be through and note some “housekeeping” matters, which isn’t always obvious to people at first. The number lottery players has no bearing on one’s individual ticket’s chance of winning. Neither does any information on what other tickets you may have played then, or at any other time. We’ll discuss lottery strategies in a later section. Note that we already solved the probability math above, and the number of lottery tickets sold to anyone was not part of our formula. Hence as a matter of math, it doesn’t matter. What we have always discussed here in this article is that the odds of a single ticket would have to win a specific prize.
Another way to reinforce what these probabilities mean, let’s think about the 197 million miles2 of earth and that humans are hypothetically homogenously spread all across the globe. Randomly pick a spot that you want (eg., the Eiffel Tower, the Taj Mahal, the location of the downed MH370 plane, the end of the Great Wall of China, the North Pole). Please imagine one small location on the globe, before continuing.
Now we carve out South America and state that if you picked a location in South America, then you have won a prize. This probability of choosing this location reflects the probability of guessing the red powerball, or 1:26.
Further, what about the probability of guessing all 5 white-balls? This is now an area of just 18 miles2. Or of all places in the world, guessing Rio de Janeiro’s Galeão International Airport. Is that what you imagined, or would eventually imagine? Didn’t think so, yet this reflects a 1:11.2 million probability outcome.
Still think you’ll be able to guess the winning region picked for the big jackpot? Think there is a “pattern” to this? You’d have to have guessed Estádio Jornalista Mário Filho, the soccer stadium of Rio. Guessing the main prize correctly means predicting a random place on earth, a place the size of a soccer field (less than 1 mile2)! And this is a 1:292 million outcome that one would have guessed this correctly!
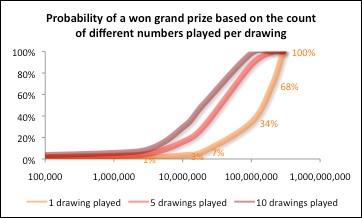
Now we shift gears from this base of probability work, and we can expand our framework in advanced ways to take into account multiple players competing for similar prizes over time. And the probability work will continue to become more fascinating! In the chart below we show the probability of someone winning the 1:292 million grand jackpot based on the number of other players also buying a different tickets, repeatedly over a certain number of drawings.
We can get to 100% probability multiple ways. The first of course is that we have 292 million players (continue to see the bright orange color curve). Another way of course is that we have 29 million people buying tickets over and over, over 10 drawings, all with no replacement (see the dark red color curve).
These are dispiriting probabilities for what it takes to win the advertised Grand Prize: after shelling out hundreds of millions on tickets (collectively by tens of millions of people over a couple handful of drawings), only improves one’s chance from near 0%, to just over 50%.
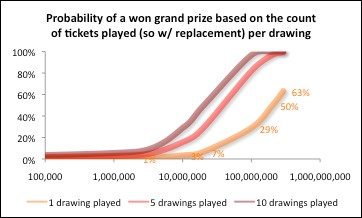
But the issue in the real world is that the tickets bought by the public are not always unique. Just like in our pick-a-spot-on-the-globe guessing game we did earlier, we often have overlaps among lottery numbers that have overlapping “special” meanings for people. If we instead consider the probability associated with randomly selected (i.e., with replacement) ticket numbers, then the probability associated with someone winning the grand jackpot stays more muted, and many more tickets played over even more drawingsneed to occur in order to have the same number of unique numbers. And therefore to achieve the same >50% probability. We can infer -from the chart below- that during January 2016’s record jackpot, hundreds of millions (of dollars) of tickets were being bought in each of those peak drawings. And then created the well-publicized >80% probability for someone to win any particular drawing at that time.
To reinforce the concepts between the two charts above, notice that in the chart immediately above that the 1-drawing bright-orange curve and the others are running lower than the same curve on the chart above that? 292 million single plays would be 100% probability of someone winning in the former chart, where as it only leads to 63% probability in the latter chart.
Rebuttal to the Lottery’s official position
For their part, the Lottery’s quants and lawyers have issued new entertaining guidance to help policy makers and potential players understand their game.
They state for example that one is more likely to win a jackpot than to be struck by lightening, except it errs in noticing that more Americans don’t go out venturing in a thunderstorm versus play the lottery, so looking at the probabilities without properly adjusting for those who try, is an error.
They also state something laughable: “That’s when you take a certain zip code, look at total lottery sales within that area, and then assume that everyone in it has the same income and refuses to play the lottery anywhere else. … It’s like saying that gasoline purchases are made mostly by poor people, because there are few gas stations in wealthy neighborhoods.” Is this a suggestion that wealthy individuals are waiting in line in a poor neighborhood’s 7-Eleven to buy lottery tickets?
Followed by something as kooky as it is dangerous: “In our stressful world, the ability to dream is well worth the price of a lottery ticket.”
Their guidance last year had other points, but neither had a comment section for citizens to voice their opinion. They had stated for example, “The rich also invest and gamble in stock and commodity markets — also activities the poor cannot afford.” But the Lottery is not and investment! We’ll see later that those investing their retirement are almost assuredly going to do better than a scheme that skims 45% off the top and taxes any winnings.
They also haughtily ranted off incoherently in other topics about not having to complete a Form 1040 (implicitly acknowledging that you aren’t going to win), to the poor having the right to entertain themselves straight into deeper poverty: “The purchase of a lottery ticket is completely voluntary – and a lot more fun than filling out Form 1040. … This question implies that economically disadvantaged people are somehow less capable of making a decision on how to spend a dollar than those of greater means or that they are not entitled to the same opportunities for entertainment and recreation than the rest of us. The poor are allowed to vote, get married, and sign contracts.”
Which brings us all to a situation where someone already poor might lose a lot of money often, and feel as if they are a problem gambler. The Multi-State Lottery Association provides as a resource this broken site. Now that’s official entertainment.
The trends and strategies in lottery wins
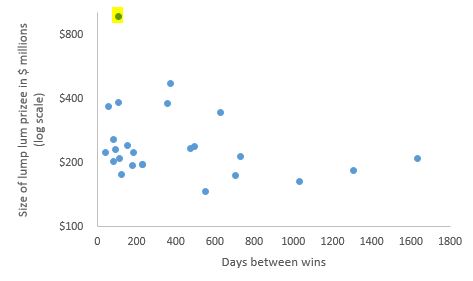
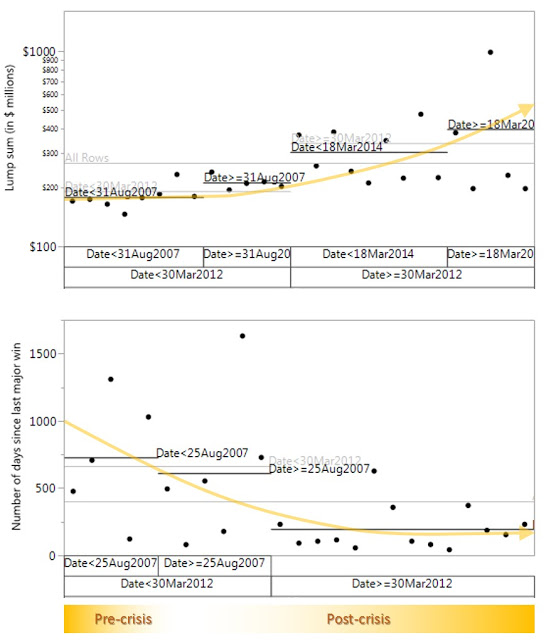
The actual time gap between the major lottery wins throughout history reveals a mild inverse relationship between the size of the jackpot and the time to have a jackpot winner. We highlight the recent January jackpot of $1.6 billion (available as a $983 million lump sum as shown) which was won 105 days after the sole winner of September’s sizeable jackpot win of $197 million.
Additionally we notice other trends in these major jackpot winnings. The amount of playing has picked up alongside the jackpot sizes, at a much faster rate, since the global financial crisis (GFC). Sure the odds are more difficult now versus before, but this only means the frequency between wins would be wider unless there was more disproportionately more playing. What we are witnessing is a consequence of, according to Discovery, “1/3 of people in the United States think winning the lottery is the only way to become financially secure in life.”
One of the intriguing probability ideas also in this lottery business is that a model can be used to determine the distribution of how often the lottery is won. This is similar to the basic concepts (discussed in depth in our Statistics Topics bestseller that is free on Amazon Prime) of the Poisson and binomial model, and the more advanced math of convolution which is the study of frequency and severity and one we even prove here has stumped famous Nobel Laureates (here, here, here). The basic result of this model that ties together all of the revenue and odds parameters we have thusfar discussed about the lottery is that the typical time needed to win the grand prize is only several drawings (by which point the jackpot size can balloon to about $75 million to $125 million). 70% of the wins occur within a few lotteries.
So equally, the other 30% shows lottery wins that take more than several drawings to achieve. And the overall typical time in-between the larger payouts (>~$300 million) for the overall system is just less than a year (<50 drawings). By making engineering the odds to have higher jackpots, which we discussed in a previous section, we should have made the winning frequencies less, however as we are noticing here the greater playing since the GFC is reflected instead in more frequent winnings of somewhat large prizes!
The idea here is that as jackpots swell (and buffeted by financial insecurity after the GFC), the wins must be arbitraged away since the pot sometimes will grow far in excess of the equilibrium amount of money we previously discussed that needs to be put into the system. So there is an economic imbalance. And enough people will play in order to guarantee a winner quickly, after the pot zooms over levels in the hundreds of millions of dollars (e.g., the >$300m jackpots shown above).
Discussing number-picking strategies
Some strategies abound concerning being owed a magic number to be generated by the Lottery. This “special number” could be derived from some divine calling, or a symbolic number such as a birthday or anniversary, or simply contrarian plays such as avoid popular birthday numbers. Would such strategy have worked in our previous example of “pick a location on the globe” quiz, earlier in this article? Of course not, yet when it comes to the Lottery people tend to believe that mythical, supernatural forces can help them.
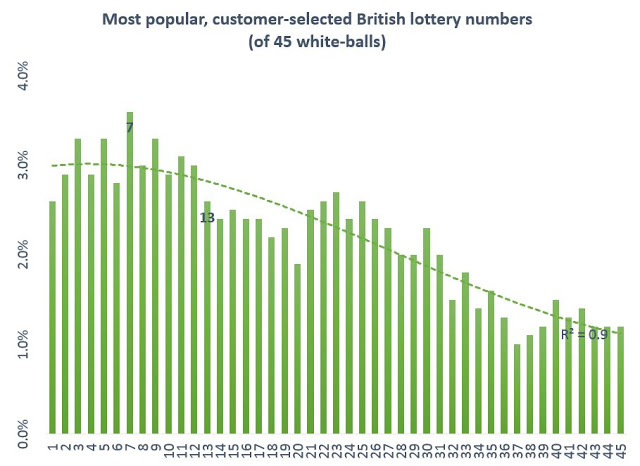
So it is true that some numbers tend to be more popular across the globe. Again the probability of any such number winning is not impacted, as we discussed in a previous section. However more people selecting a popular number –when that number happens to win- will receive a smaller share of the jackpot prize as it is of course split among more winner. In the chart below, constructed from data Professor Tijms showed in the University of Cambridge book “Understanding probability”, we see that in the British lotteries there are some “patterns” among popular customer lottery number picks.
Lucky 7 is the most popular (in other studies there has been a slight uplift relative to neighboring numbers for all numbers ending in “7” such as 17, 27, 37, 47), and unlucky 13 is unpopular. Birthday numbers (e.g., 1-30) are more popular then numbers >30. Finally per Benford’s law of naturally occurring numbers, the smaller single-digit numbers tend to be quite popular (e.g., if one finds the number “5” special and can’t select any numbers in the 50s, then they might instead select “5” as opposed to a 2-digit number ending in “5”). Notice that the downward trend in popularity after the first ten or so digits has a high R2 fit?
This is the same concept (though likely with less impact) as being economically advantageous. Again the odds won’t change, but one would want to only be playing the unpopular numbers (e.g., those in the upper third of the number range) and during large jackpots. Still all of these gambling improvements may only increase your economic advantage by far less than the magnitude of the 45% skim that the Lottery takes off the top. Recall that you could play nearly 400 million dollars’ worth of play (and unless you have multiple grocery stores ensure you get all those different tickets printed up within a few days) in the current lottery system ($2/ticket) you would still have a 50% chance of not winning!
200 million tickets at a 1/10 second a ticket is 20 million seconds (231 days). You would need to be at 77 stores to print tickets just for you at this speed around-the-clock and never have any of these stores print a duplicate number combination of any of the other stores.
Let’s pull back for a minute to make sure that we are not losing the sight of the forest through the trees. We see from the Lottery revenue data that most regular adult players will play ~$30 a drawing. At 2 drawings weekly, for 45 adult years, we come to $135k in after-tax money wasted, over an adult lifetime. So let’s discuss a final irony concerning this.
A final irony
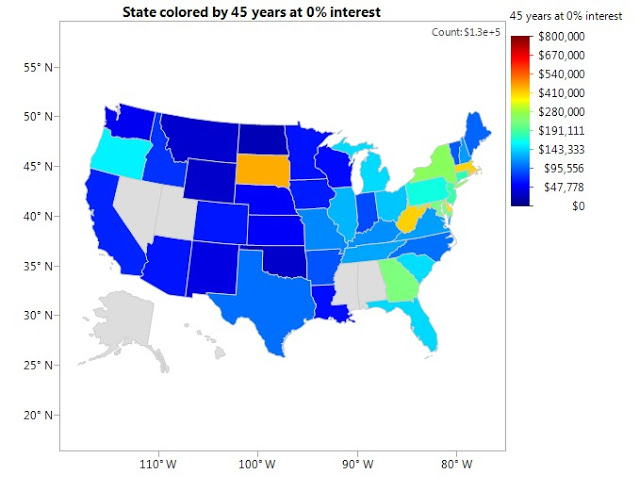
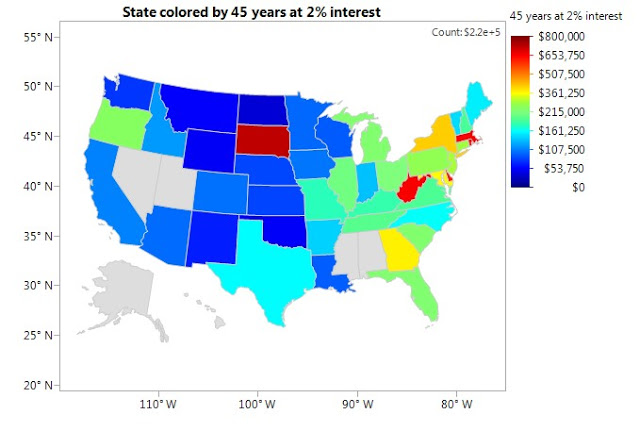
We noted above the typical adult player will waste $135k. This does not imply the median spending of anyone who will have ever played lottery in their life! An incredible portion of American adults (~95%) will either never play, or will play such a small fraction of this level. But there is a minimal number that will be regulars, who bring in nearly ½ the total revenue to keep this system afloat, and will be the ones who play nearly $135k in a lifetime. Averaging the level of play among all people who ever play, we could still get to over $25k in a lifetime. Both of these statistics are significant, as per the Federal Reserve (page 12), the median net worth of a family approaching retirement is $166k (per individual adult it would be nearly half this).
So imagine that. One could have their nest egg guaranteed to be enlarged by $135k, instead of religiously trying to score a million-dollar mirage and instead being stuck poor. And if one were instead save this money at a conservative 2% rate of return, then they would have by retirement age $215k just from these lottery savings. Enough to pay for 4-years of private college tuition, or a small home in a rural part of the country, or a lifetime annuity of >$500 monthly.
One will also notice in these charts the same heterogeneity in adult playing levels across the U.S. In Massachusetts and neighboring Rhode Island for example, the typical adult who has ever played lottery, wastes nearly $20/drawing over their lifetime (3 times the national average). And the payouts there we showed in the first section is not always larger for these states. And their lifetime spending (savings accruing at a modest 2%annually) for all players in these states, equivalently comes to ~130k. And >$650k for the serial players. Incredible sums that can work out to several multiples of one’s salary, and ironically more than the million-dollar prize, after-taxes.
Source: Statistical Ideas